Hamilton Decompositions of Cayley Graphs on Abelian Groups

Brian Alspach, School of Mathematical and Physical Sciences, University of Newcastle, Australia
Cafer Caliskan, Department of Mathematical Sciences, Michigan Technological University, U. S. A.
Donald L. Kreher, Department of Mathematical Sciences, Michigan Technological University, U. S. A.

Contents

1  Summary
2  Project Description
    2.1  Background
    2.2  Goals
3  preprints

1  Summary

This is an ongoing research project to study when a Cayley graphs on an abelian groups has a Hamilton decomposition. If A s an abelian group and S ⊂ A such that 0 ∉ S, then the inverse-closure S∗ of S is the smallest superset of S satisfying s ∈ S∗ if and only if −s ∈ S∗.
The Cayley graph Cay(A;S∗) is the graph whose vertices are the elements of A with x adjacent to y if and only if x−y ∈ S∗. The set S∗ is called the connection set.
A cycle that spans the vertices of a graph X is called a Hamilton cycle of X. A Hamilton decomposition of a regular graph with even valency is a partition of its edge set into Hamilton cycles. A Hamilton decomposition of a regular graph with odd valency is a partition of its edge set into Hamilton cycles and a single one-factor. A graph admitting a Hamilton decomposition is said to be Hamilton-decomposable. Alspach conjectured the following in 1984:
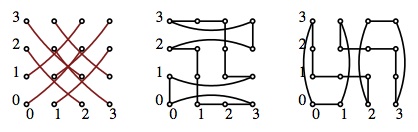
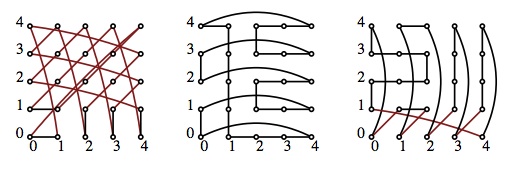
connected Cayley graphs on abelian groups are Hamilton-decomposable.
This conjecture remains unresolved. The proposer Alspach (joint work) recently verified the conjecture for the family of Paley graphs. The proposers Caliskan and Kreher substantially extended the preceding result by showing that odd order 2(n+1)-regular connected Cayley graphs of rank n elementary abelian groups are Hamilton decomposable. The method used looks very promising and the proposers' goals have five stages. The first stage is to remove a restrictive condition on a result of Liu involving Cayley graphs on even order abelian groups. The second stage is to extend a recent result of Westlund, Liu and Kreher on Cayley graphs on odd order abelian groups to all orders. The third and fourth stages are to extend the method mentioned above to Cayley graphs on elementary abelian groups with arbitrary connection set. The fifth stage is to settle the conjecture for abelian groups of prime power order. We intend to make these dramatic inroads on the general conjecture using the fact that elementary abelian groups are a fundamental building block in the construction of abelian groups.

2  Project Description

2.1  Background

Let A be an abelian group and S ⊂ A such that 0 ∉ S. We denote by S∗ the inverse-closure of S, that is, S∗ is the smallest superset of S satisfying s ∈ S∗ if and only if −s ∈ S∗.
The Cayley graph Cay(A;S∗) is the graph whose vertices are the elements of A with x adjacent to y if and only if x−y ∈ S∗. The subset S ⊆ A is called the connection set for the Cayley graph Cay(A;S∗) and an edge {x,y} of Cay(A;S∗) is an s-edge if x±s = y, for s ∈ S.
A cycle that spans the vertices of a graph X is called a Hamilton cycle of X. A Hamilton decomposition of a regular graph with even valency is a partition of its edge set into Hamilton cycles. A Hamilton decomposition of a regular graph with odd valency is a partition of its edge set into Hamilton cycles and a single one-factor. A graph admitting a Hamilton decomposition is said to be Hamilton-decomposable (see Figures 1 and 2).
Fig1.jpg
Figure 1: A Hamilton decomposition of Cay(Z52;{ (1,1),(0,1), (1,0) }∗)
Fig2.jpg
Figure 2: A Hamilton decomposition of Cay(Z42;{ (2,2),(0,1), (1,0) }∗)
This project focuses on a conjecture of Alspach from 1982, first appearing in print in 1984 [1], which asserts that connected Cayley graphs on abelian groups are Hamilton-decomposable. This conjecture remains unresolved.
Bermond [3] conjectured in 1978 that the cartesian product of Hamilton-decomposable graphs with even valency is Hamilton-decomposable. Bermond's Conjecture does not mention Cayley graphs on abelian groups, but it definitely is germane to any discussion of Alspach's conjecture. There are good reasons for this as explored below.
Bermond's Conjecture also remains unresolved, but there is a very useful partial result due to Stong [10]. Stong's result includes, for example, the following theorem.
Theorem 1 If X1 is a Hamilton-decomposable graph of valency 2r and X2 is a Hamilton-decomposable graph of valency 2s, with r ≤ s, then the cartesian product X1[¯] X2 is Hamilton-decomposable if either of the following two conditions holds:
  1. s ≤ 3r, or
  2. r ≥ 3.
Cayley graphs on abelian groups frequently contain spanning subgraphs that either are cartesian products or close to being cartesian products (called pseudo-cartesian products in [7]). Thus, positive results on Bermond's Conjecture frequently are helpful when dealing with Alspach's Conjecture.
In addition, some of the methods employed by Stong transfer directly to Cayley graphs on abelian groups. This adds to the connections between the two conjectures
There have been two avenues of approach used in the attack on Alspach's Conjecture. One approach has been a step-by-step induction with respect to the valency of the Cayley graphs, and the other approach has centered on examining connection sets with special structure. We discuss both approaches.
The valency approach begins with the following trivial result. Its proof is immediate using the well-known fact that every connected Cayley graph on an abelian group contains a Hamilton cycle.
Theorem 2 Every connected Cayley graph of valency 2 or 3 on an abelian group is Hamilton-decomposable.
The first substantial result was obtained in 1989 by Bermond, Favaron and Maheo [4] who proved the next result.
Theorem 3 Every connected Cayley graph of valency 4 on an abelian group is Hamilton-decomposable.
For graphs of valency 6, a result was recently obtained by Westlund, Liu and Kreher [11].
Theorem 4 Every connected Cayley graph of valency 6 on an odd order abelian group is Hamilton-decomposable.
A preprint received from Westlund [12] reports that he has extended the above theorem and has obtained the following result.
Theorem 5 Every connected Cayley graph of valency 6 on an even order abelian group in which the connection set contains an element generating a cyclic subgroup of index 2 is Hamilton-decomposable.
The aforemention results are as far as the valency approach has gone. Note that even with valency 6 complete results are limited to Cayley graphs on odd order abelian groups. Even order groups raise barriers that are not present for the odd order case.
The most substantial positive result following the avenue of considering connection sets with special structure arises from a series of three papers by J. Liu [8,9], where we have cited only the two most recent because the initial paper is subsumed by [8]. Recall that S∗ denotes the inverse-closure of S. The following theorem summarizes Liu's very nice work.
Theorem 6 If G is an abelian group and S is a minimal generating set of G, then Cay(G;S∗) is Hamilton-decomposable as long as 2s ∉ S for s ∈ S when |G| is even.
The proof method employed by Liu to achieve Theorem 6 is a clever and technically complicated extension of the method employed by Stong to prove Theorem 10. This establishes another connection with Bermond's Conjecture.
The three PIs have been involved in some recent progress on the conjecture under discussion. The PI Alspach, working jointly with D. Bryant and D. Dyer, has proven that all Paley graphs have Hamilton decompositions [2]. Recall that the Paley graph of prime power order q, q ≡ 1(mod 4), is the graph whose vertices are the elements of the finite field of order q, where two vertices are adjacent if and only if their difference is a quadratic residue in the field. The most interesting feature of the proof is a strong dependence on the well-known matroid partition theorem of Edmonds and Fulkerson [6]
Of course, Paley graphs are Cayley graphs on elementary abelian p-groups. Realizing that elementary abelian groups are fundamental to the structure of abelian groups, proposers Caliskan and Kreher took a different approach in 2011. They establish the following result in  [5].
Theorem 7 Let S be a basis of V=Zpn, p an odd prime, and let g be any non-zero vector of V \S. Then the Cayley graph X=Cay(V;(S∪{g})∗) has a Hamilton decomposition.
Their proof is an induction proof on the rank of the abelian group that begins with rank 2. They include an application of the Theorem 7 to Paley graphs and show that when given a prime power q=pn and an even order rank n multiplicative subgroup S of the finite field Fq, the Cayley graph with connection set S is Hamilton-decomposable, whenever |S| ≥ 2n2. This extends the recent result of Alspach, Bryant and Dyer on Paley graphs.

2.2  Goals

Our major goal for this project is to settle the Alspach Conjecture. However, the conjecture has been around for essentially thirty years and leaving the goal just stated standing alone might appear presumptuous on the part of the proposers. Consequently, we have laid out a sequence of more modest subgoals. This is an important positive feature of this project.
By setting forth a sequence of subgoals, we have established a plausible approach to the main conjecture. The subgoals themselves are of sufficient interest that upon successful resolution at least one publication would be forthcoming. Techniques and ideas developed for the subgoals will be applicable to the resolution of the main conjecture.
Subgoal 1.
We wish to improve Theorem 6 by eliminating the condition that 2s ∉ S for s ∈ S, thereby, establishing the theorem for all minimal generating sets.
Subgoal 2.
We wish to extend Theorem 7 to Cayley graphs on even order abelian groups.
Subgoal 3.
We wish to extend Theorem 7 to Cayley graphs on rank n elementary abelian groups with valency d > 2(n+1)
Subgoal 4.
We wish to extend Theorem 7 to Cayley graphs on arbitrary rank n abelian groups.
Subgoal 5.
We want to show that the conjecture holds for abelian groups of prime power order.
Subgoal 1 requires a careful look at Liu's proof and a possible generalization of the method used in [2] of boosting the valency in some of the component graphs of a cartesian product. We believe there is an excellent chance of realizing subgoal 1 within the first year of the project.
Subgoal 2 is in the same spirit as subgoal, 1 but is more difficult and little already done. Nevertheless, while trying to complete the work for subgoal 1, we shall keep subgoal 2 in mind because the difficulties brought forth by working with even order groups manifests itself in both problems.
We already have made substantial progress on subgoal 3. This subgoal most likely will be achieved early. It should be the first subgoal attained.
We also have made good progress on subgoal 4. It also could be done fairly early in the life of the project.
Subgoal 5 is more ambitious and will take some development. PI Alspach obtained a few partial results on this subgoal about eight months ago and set the project aside at that time. He looks forward to getting back to this subgoal with the additional manpower involved in the project.
The completion of the five subgoals would lead us to the final step of looking at the full conjecture. Mathematics projects are completely different from lab projects. One can attempt to plan an attack on a hard problem, but we believe that success frequently arises from something totally unexpected. Also, as with any mathematics research project, it is never clear what the actual results will be and while pursuing the above goals we may find avenues of related research that are more fruitful. We reserve the right to pursue such avenues, indeed, we feel it is important to do so.

References

[1]
B. Alspach, Research Problem 59, Discrete Math. 50 (1984), 115.
[2]
B. Alspach, D. Bryant and D. Dyer, Paley Graphs Have Hamilton Decompositions, Discrete Math., to appear. Cycles and Rays,
[3]
J.-C. Bermond, Hamilton decomposition of graphs directed graphs and hypergraphs, Advances in Graph Theory, Annals of Discrete Math. 3 (1978) 21-28.
[4]
J.-C. Bermond, O. Favaron and M. Maheo, Hamiltonian decomposition of Cayley graphs of degree four, J. Combin. Theory Ser. B 46 (1989), 142-153.
[5]
C. Caliskan and D. L. Kreher, Odd order 2(n+1) regular connected Cayley graphs on rank n elementary abelian groups are Hamilton decomposable Disctrete Math. Submitted (2011).
[6]
J. Edmonds and D. R. Fulkerson, Transversals and matroid partition, J. Res. Nat. Bur. Standards Sect. B 69B (1965), 147-153.
[7]
C. Fan, D. R. Lick and J. Liu, Pseudo-Cartesian product and Hamiltonian decompositions of Cayley graphs on abelian groups, Discrete Math. 158 (1996), 49–-62.
[8]
J. Liu, Hamiltonian decomposition of Cayley graphs on Abelian groups of odd order, J. Combin. Theory Ser. B 66, (1996), 75-86.
[9]
J. Liu, Hamiltonian decompositions of Cayley graphs on abelian groups of even order, J. Combin. Theory Ser. B 88 (2003), 305–-321.
[10]
R. Stong, Hamilton decompositions of Cartesian products of graphs, Discrete Math. 90 (1991), 169-190.
[11]
E. Westlund, D. Kreher and J. Liu, 6-regular Cayley graphs on abelian groups of odd order are hamiltonian decomposable, Discrete Math. 309 (2009), 5106-5110.
[12]
E. Westlund, Hamilton decompositions of certain 6-regular Cayley graphs on abelian groups with a cyclic subgroup of index two, preprint.

3  preprints

  1. C. Caliskan and D.L. Kreher, Odd order 2(n+1) regular connected Cayley graphs on rank n elementary abelian groups are Hamilton decomposable


File translated from TEX by TTHgold, version 4.00.
On 26 Sep 2011, 17:13.